Positive/Negative Count Frequencies

Do we spend more time in positive or negative counts?

This is not a particularly useful page — but the question comes up now and again and the answer is more complex than might be supposed. It feels as though the true count spends more time in negative territory than positive territory. Is this true? First, if you floor counts, this is clearly true as you always integerize the count downward. But suppose you truncate, which would round positive counts down and negative counts up? And suppose you calculate the remaining cards in the shoe exactly and don't use a cut-card, removing effects of estimation and the cut-card effect (discussed in a later chapter)?

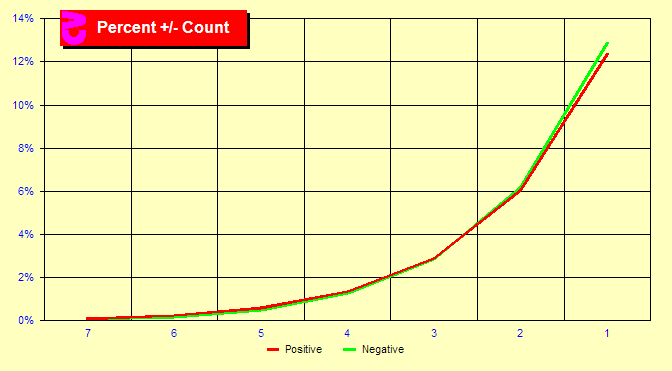
The chart at the right is like the earlier True Count Frequencies chart, except that it has been folded in half to better compare the positive and negative counts. The red line shows the positive true counts for counts with magnitudes of 1 through 7, and the green line shows the negative counts for the same magnitudes. What we see in this chart is a greater number of -1 then +1 counts.

What are the percentages?

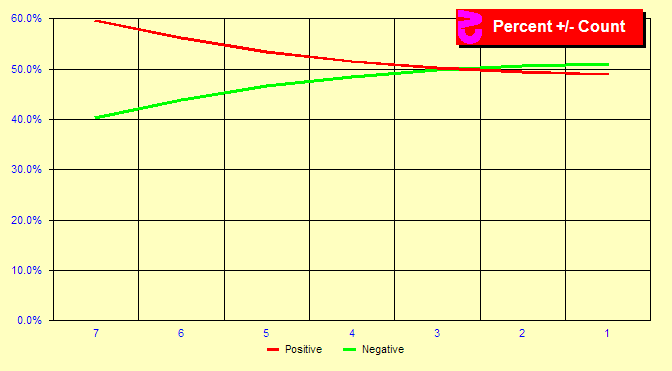
It is difficult to see the differences in larger magnitude counts in the first chart. To get a better look at these counts, let us take the exact same data but create a percentage chart. In this chart, we see that 60% of true counts of magnitude 7 are positive and 40% negative. Substantially more high positive counts exist than low negative counts of the same magnitude. But then, few counts of that large a magnitude occur at all. On the other hand, somewhat more counts of -1 and -2 occur than +1 and +2.

What does it all mean?

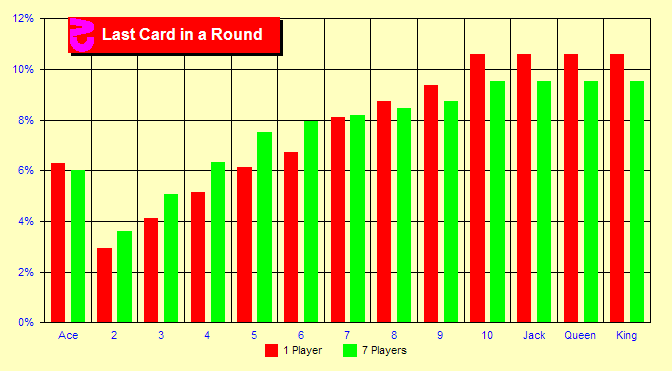
Why is this? In this chart, we will look at the frequencies of the last card dealt in a round assuming one and seven players. What we see is that the last card dealt is more likely to be a high card than a low card. This is not surprising as a ten is more likely to cause a bust or final hand, but a deuce is likely to call for another draw. The number of players affects these percentages because the dealer follows different rules than a Basic Strategy player. Since the most common count is zero, and the most common last card dealt in a round is high, more -1 counts exist than +1 counts at the start of a round. On the other hand, when a round contains small cards, it often contains many small cards as small cards can result in hands with many cards. This is why more counts of +7 exist than -7.

The True Count Theorem tells us that at the end of every round, on average the true count will be zero. Does this violate the TC Theorem? No. Because although the number of rounds starting with a negative count is greater than the number of rounds starting with a positive count, the average count is still zero. The excess negatives at -1 and -2 balance the excess positives at +3 and higher. The TC Theorem does not say that the distribution of negative and positive counts is the same.

Sim details

• Six decks, S17, DAS, LS, fixed rounds, Hi-Lo max indexes, trunc, exact cards
• One and seven players
• Two billion rounds each