by Norm Wattenberger
Effect of Blackjack True Count Methods
|
|
Another area of variability in true count calculation is the method
of integerization after dividing the running count by remaining decks.
Nearly all Blackjack card counters use integer true counts. When you
divide 5 by 3, how do you turn this into an integer? (Most Blackjack
books give easy examples like 6/3 and fail to touch on the question.)
Some people round to the nearest integer (rounding), some always round
down (flooring) and some round towards zero (truncation). Truncation
is a bit less accurate because it greatly increases the number of
zero counts. This reduces the resolution of the count. Rounding and
flooring have about the same overall accuracy. As the chart shows,
flooring and truncating have the same advantages at positive counts
because they both round down at positive counts. But this changes
below the zero count since truncation now rounds up. This means that
truncated counts below zero will have a lower advantage. See the follwing
graph for the details. |
|
If you integerize True Counts in different manners, the frequencies
of those true counts will change. This chart provides the frequencies
for the three methods of integerization. The green and red lines (flooring
and truncation) are identical for counts of +1 and higher. The red
line indicates a very large percentage (42%) of counts of zero for
truncation. This is because all counts between -.999 and .999 will
truncate to zero. Truncation is a bit inferior due to this large peak
at TC zero. When you have so many hands all identified as a count
of zero, the count is less precise and an index of zero less valuable.
However, the overall effect on advantage is not high. |
|
Sim details
|
copyright © 2007, 2024, Norm Wattenberger, All rights reserved
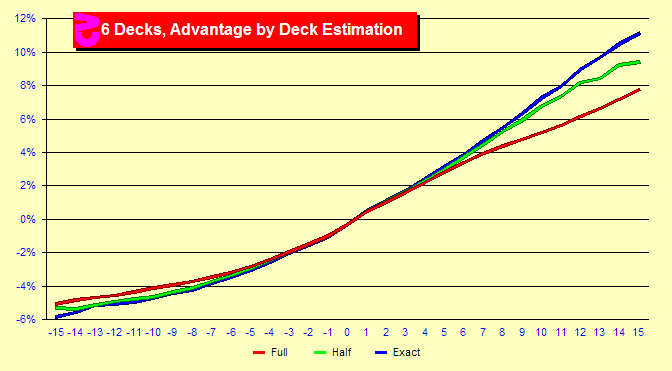 How
do different manners of True Counting differ?
How
do different manners of True Counting differ?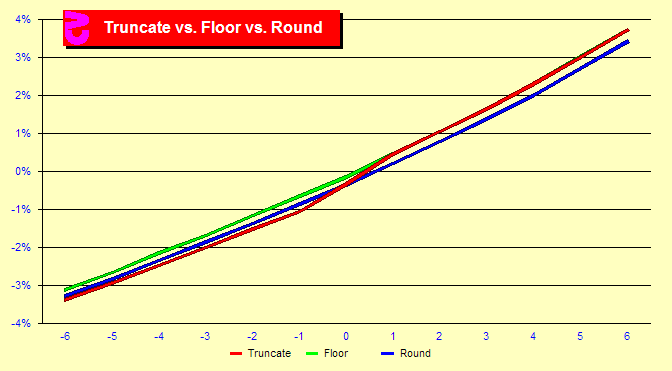 What
about division rounding methods?
What
about division rounding methods?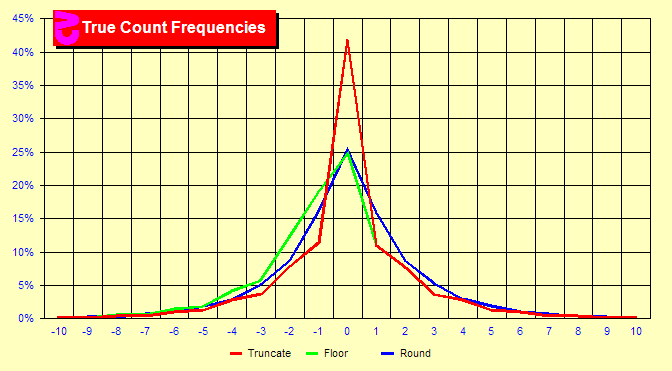 How
does this affect count frequencies?
How
does this affect count frequencies?