Chapter 6. Cover Data

"You Can't Get There from Here" — Ogden Nash, 1957

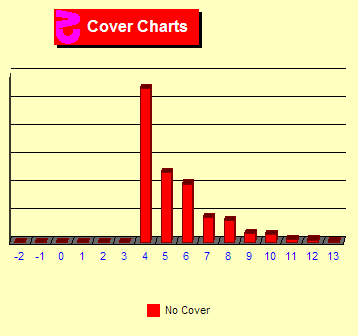How does cover betting affect max bets?

To avoid looking like a card counter and being barred from Blackjack play, many players add cover to their betting. That is they bet more like average players than counters. Obviously not betting optimally will reduce your expected results. In these charts, I am assuming a six-deck game with four players and a simple betting scheme of 1, 2, 4, 8, 16 units at true counts of <=0, 1, 2, 3, >=4. I start with no cover and then add one typical cover betting rule at a time. The charts show only the number of max bets (16 units) made at each true count.

We start with a chart that shows no cover in red. The red bars show that there are zero max bets below TC +4. At TCs +5 and higher there are fewer and fewer max bets because there are fewer hands at higher TCs. All hands of counts +4 and above are played with max bets. This provides our benchmark.

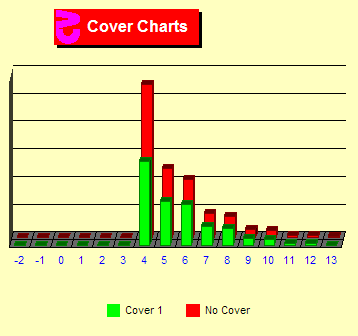Cover 1 – No increase after a loss

Four types of cover will be added cumulatively. The first cover rule used is "no increase after a loss." With this cover method, units bet cannot be increased after losing a hand no matter what the count. The majority of average players bet in this manner. If you raise after a loss inconsistently, you might indicate to the casino that you are counting.

The green bars still shows zero max bets below TC +4. But, a much smaller number of max bets are made at TC +4 since the player is not increasing the bet after a loss even if the TC increases. There are fewer max bets at higher TCs also, but the red and green bars grow closer since the TC is less likely to make large increases. The cost in this instance is underbetting when the count is high. And the cost can be high since the entire point of card counting is to bet high when the count is high.

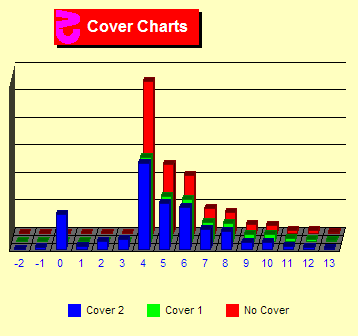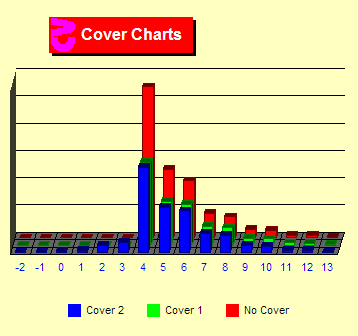Cover 2 – No decrease after a win

In these charts, I add the "no decrease after win" rule. This is the blue set of bars. There are two charts here and later on this page depending on the player's actions at the start of a shuffle. In the left chart the player always drops to one unit after a shuffle. In the right chart, the player follows the cover rules. For example, suppose you bet 16 units on the previous hand and you won. The cover rule says that you will not decrease your bet after a win. So you would bet 16 units even if the count dropped in the right-hand chart. However, some people use the shuffle as an excuse to ignore the cover rule and always drop to one unit — the correct bet. This looks OK in shoe games but is harder to get away with in single-deck.

At TCs +4 and above, we see about the same number of bets as not using this rule. But, now we see that max bets are being made at TCs +2 and +3. That is, we are sometimes overbetting at these counts. In the right-hand chart, we also see max bets at TC 0 since we will sometimes not be able to reduce our bet at the start of the shoe. This is very costly since there is negative EV at TC 0.

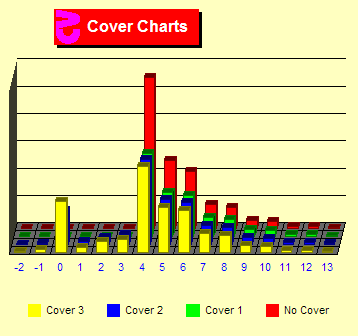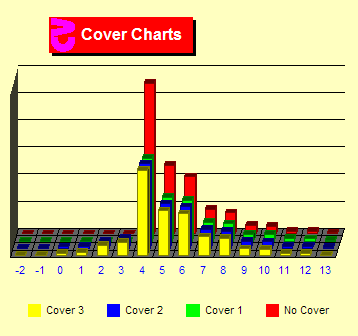Cover 3 – Same bet after push

Now let's add the "same bet after push" rule. Few players change their bets after a push since there is already a bet up. The yellow bars in the charts indicate even more overbetting at TCs +3 and +2 and below since the rule does not allow us to change our bet after a push even if the count changes.

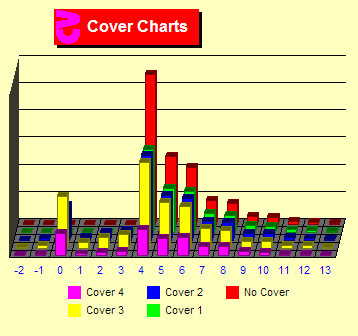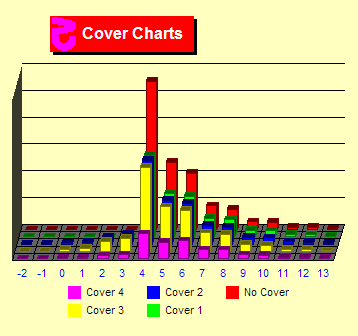Cover 4 – No large increases or decreases

OK, let's add a "no large bet changes" rule. With this rule we cannot jump bets, like jumping from 2 to 8 or 16 to 4 units. This is depicted by the set of violet bars. Here we show a dramatic decline in max bets at TC +4. And, to a lesser but very significant degree, further decreases in max bets at TCs +5 and above. This rule is very costly when the count changes a great deal from hand to hand. Large changes in count are more likely at full tables or single-deck.

If we use all of the rules, we can see that we are betting our maximum amount far less often at high counts than we should and at times bet the max amount with a negative expectation. Clearly, religious adherence to full cover is not practical.

Sim details

• Six decks, S17, DAS, LS, 4 players, Hi-Lo max indexes, 4.8/6 Penetration
• Eight degrees of cover
• One billion rounds each